Dieser Artikel bringt Euch eine Erfindung am Rande des Bitcoin-Universums näher, nämlich den „Merkle Tree“ oder auf deutsch „Hash-Baum“.
Laut deutscher Wikipedia (Artikel: https://de.wikipedia.org/wiki/Hash-Baum) lautet die Erläuterung wie folgt: „Ein Hash-Baum (englisch hash tree oder Merkle tree, nach dem Wissenschaftler Ralph Merkle) ist eine Datenstruktur in der Kryptographie und Informatik. Ein Hash-Baum ist ein Baum aus Hashwerten von Datenblöcken, beispielsweise von einer Datei. Hash-Bäume sind eine Erweiterung von Hash-Listen und dienen gleichermaßen dazu, die Integrität von Daten sicherzustellen.“
Was ist der Sinn und Zweck dieser Konstruktion? Ein kurzer Rückblick in den Aufbau einer Blockchain zeigt uns, das in einem Block viele Transaktionen enthalten sind und „in einem Rutsch“ verarbeitet werden. Jede dieser Transaktionen hat einen eigenen Transaktions-Hashwert – aber wie kann ich einfach und schnell sicherstellen, das mein Block auch alle Transaktionen beinhaltet, ohne die Datenmenge aufzublähen? Die Antwort liegt im Merkle Tree, der wie ein „umgekehrt“ wachsender Baum aufgezeichnet wird und ganz oben nur noch ein Element hat, die Wurzel oder „Root“. Der Hashwert dieses Wurzelelementes ist im Datensatz des Blockes verankert und wiederum ein Teil des Block-Hashwertes und damit vor nachträglichen Änderungen geschützt.
Wie wird nun ein Merkle Tree aufgebaut? Schauen wir uns eine Grafikdarstellung eines einfachen Baumes an (die Werte wurden mit dem nachfolgenden Testprogramm errechnet und sind damit auch nachvollziehbar):

Fangen wir unten an: wir haben insgesamt 8 Rohwerte („1“ bis „8“) und wir möchten sicherstellen, das alle 8 Rohwerte in unserem Baum enthalten sind. In Runde 1 bilden wir von jedem Rohwert des Hashwert. Wir nutzen hier das CRC32-Verfahren, da es uns ein kurzes Ergebnis liefert. Beim Bitcoin wird an dieser Stelle das SHA256-Hash Verfahren genutzt. Um an die Ergebnisse von Runde 2 zu gelangen, füge ich einfach die beiden CRC32-Werte vom Rohwert „1“ = „83dcefb7“ und Rohwert „2“ = „1ad5be0d“ zu einem neuen String „83dcefb71ad5be0d“ zusammen und bilde davon dann den CRC32-Hashwert „d658193f“. So verfahre ich mit allen Werten und am Ende (also ganz oben) erhalte ich den Wurzel- oder Root-Wert „686159e3“. Sollte der Merkle Tree nicht die exakt passende Anzahl an Rohwerten enthalten gibt es einfache Regeln, die für eine passende Anzahl sorgen.
Wie kann ich nun eine einfache Prüfroutine aufbauen, welche mir die gewünschte Bestätigung gibt, das „mein“ Rohwert auch im Merkle Tree beinhaltet ist? Schauen wir uns das zweite Bild an, bei dem die passenden Felder farblich eingefärbt sind:
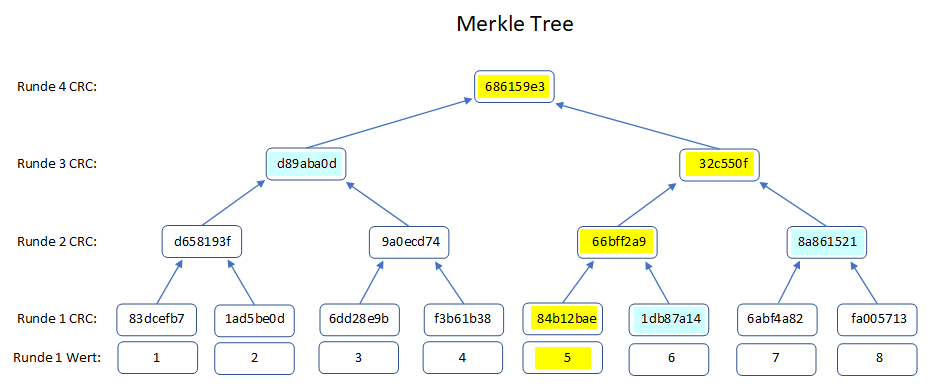
Nehmen wir an, das sich unsere Frage auf das Rohelement „5“ bezieht. Dann liefert mir die sogenannte „Proof-Routine nur 3 weitere Werte: ich bekomme die Wertkombinationen „rechts 1db87a14“, „rechts 8a861521“ und „links d89aba0d“ genannt. Damit kann ich wieder die einzelnen CRC32-Hash Werte berechnen und komme am Ende zu meinem Root-Element „686159e3“. Die Worte „rechts“ und „links“ beziehen sich darauf, ob dieser Wert auf der rechten oder linken Seite der String-Zusammenfügung bezieht. Somit kann ich in 4 Schritten selber errechnen, das „mein“ Rohwert tatsächlich im gesamten Hash-Baum enthalten ist.
Natürlich ist es wichtig, das die verwendete Hashfunktion „einzigartige“ Werte liefert und die Funktion kryptografisch ungebrochen ist (daher noch einmal der Hinweis: die CRC32-Methode dient nur der Veranschaulichung, sollte aber nicht für „echte“ Bäume eingesetzt werden).
Hier nun das Programm und die Ausgabe auf der Konsole:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
/* * Herkunft/Origin: http://javacrypto.bplaced.net/ * Programmierer/Programmer: Michael Fehr * Copyright/Copyright: frei verwendbares Programm (Public Domain) * Copyright: This is free and unencumbered software released into the public domain. * Lizenttext/Licence: <http://unlicense.org> * getestet mit/tested with: Java Runtime Environment 11.0.6 x64 * verwendete IDE/used IDE: intelliJ IDEA 2019.3.4 * Datum/Date (dd.mm.jjjj): 05.05.2020 * Funktion: erzeugt einen Merkle Tree mittels CRC32 Hashfunktion * Function: create a Merkle Tree with CRC32 hashfunction * Beschreibung in / Description in * http://javacrypto.bplaced.net/f03-sha-256-und-sha-512-hash-von-einer-datei/ * * Sicherheitshinweis/Security notice * Die Programmroutinen dienen nur der Darstellung und haben keinen Anspruch auf eine korrekte Funktion, * insbesondere mit Blick auf die Sicherheit ! * Pruefen Sie die Sicherheit bevor das Programm in der echten Welt eingesetzt wird. * The program routines just show the function but please be aware of the security part - * check yourself before using in the real world ! * */ import java.util.zip.CRC32; public class MerkleTreeSimpleCrc32 { public static void main(String[] args) { System.out.println("Merkle Tree mittels CRC32"); System.out.println("\nRunde 1"); // setup data String[] dataRound1 = {"", "1", "2", "3", "4", "5", "6", "7", "8"}; String[] dataCrc32Round1 = new String[9]; for (int i = 1; i < 9; i++) { dataCrc32Round1[i] = crc32(dataRound1[i]); System.out.println("Nr: " + i + " data: " + dataRound1[i] + " CRC32: " + dataCrc32Round1[i]); } System.out.println("\nRunde 2"); // combine data String[] dataRound2 = new String[5]; String[] dataCrc32Round2 = new String[5]; dataRound2[1] = dataCrc32Round1[1] + dataCrc32Round1[2]; dataRound2[2] = dataCrc32Round1[3] + dataCrc32Round1[4]; dataRound2[3] = dataCrc32Round1[5] + dataCrc32Round1[6]; dataRound2[4] = dataCrc32Round1[7] + dataCrc32Round1[8]; for (int i = 1; i < 5; i++) { dataCrc32Round2[i] = crc32(dataRound2[i]); System.out.println("Nr: " + i + " data: " + dataRound2[i] + " CRC32: " + dataCrc32Round2[i]); } System.out.println("\nRunde 3"); // combine data String[] dataRound3 = new String[3]; String[] dataCrc32Round3 = new String[3]; dataRound3[1] = dataCrc32Round2[1] + dataCrc32Round2[2]; dataRound3[2] = dataCrc32Round2[3] + dataCrc32Round2[4]; for (int i = 1; i < 3; i++) { dataCrc32Round3[i] = crc32(dataRound3[i]); System.out.println("Nr: " + i + " data: " + dataRound3[i] + " CRC32: " + dataCrc32Round3[i]); } System.out.println("\nRunde 4"); // combine data String[] dataRound4 = new String[2]; String[] dataCrc32Round4 = new String[2]; dataRound4[1] = dataCrc32Round3[1] + dataCrc32Round3[2]; for (int i = 1; i < 2; i++) { dataCrc32Round4[i] = crc32(dataRound4[i]); System.out.println("Nr: " + i + " data: " + dataRound4[i] + " CRC32: " + dataCrc32Round4[i]); } System.out.println("\nMerkle Root Tree: " + dataCrc32Round4[1]); System.out.println("\nProof fuer data [5] in Runde 1"); String[] proof = new String[5]; proof[1] = crc32((dataCrc32Round1[5] + dataCrc32Round1[6])); System.out.println("Runde 1: CRC32 data[5]: " + dataCrc32Round1[5] + " CRC32 data[6]: " + dataCrc32Round1[6] + " CRC32: " + proof[1]); System.out.println("\nProof fuer data [5] in Runde 2"); proof[2] = crc32(proof[1] + dataCrc32Round2[4]); System.out.println("Runde 2: CRC32 proof[1]: " + proof[1] + " CRC32 data[7+8]: " + dataCrc32Round2[4] + " CRC32: " + proof[2]); System.out.println("\nProof fuer data [5] in Runde 3"); proof[3] = crc32(dataCrc32Round3[1] + proof[2]); System.out.println("Runde 3: CRC32 proof[1-4]: " + dataCrc32Round3[1] + " CRC32 proof[2]: " + proof[2] + " CRC32: " + proof[3]); System.out.println("\nMerkle Tree Root Wert: " + proof[3]); } private static String crc32(String input) { CRC32 crc = new CRC32(); crc.update(input.getBytes()); return Long.toHexString(crc.getValue()); } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
Merkle Tree mittels CRC32 Runde 1 Nr: 1 data: 1 CRC32: 83dcefb7 Nr: 2 data: 2 CRC32: 1ad5be0d Nr: 3 data: 3 CRC32: 6dd28e9b Nr: 4 data: 4 CRC32: f3b61b38 Nr: 5 data: 5 CRC32: 84b12bae Nr: 6 data: 6 CRC32: 1db87a14 Nr: 7 data: 7 CRC32: 6abf4a82 Nr: 8 data: 8 CRC32: fa005713 Runde 2 Nr: 1 data: 83dcefb71ad5be0d CRC32: d658193f Nr: 2 data: 6dd28e9bf3b61b38 CRC32: 9a0ecd74 Nr: 3 data: 84b12bae1db87a14 CRC32: 66bff2a9 Nr: 4 data: 6abf4a82fa005713 CRC32: 8a861521 Runde 3 Nr: 1 data: d658193f9a0ecd74 CRC32: d89aba0d Nr: 2 data: 66bff2a98a861521 CRC32: 32c550f Runde 4 Nr: 1 data: d89aba0d32c550f CRC32: 686159e3 Merkle Root Tree: 686159e3 Proof fuer data [5] in Runde 1 Runde 1: CRC32 data[5]: 84b12bae CRC32 data[6]: 1db87a14 CRC32: 66bff2a9 Proof fuer data [5] in Runde 2 Runde 2: CRC32 proof[1]: 66bff2a9 CRC32 data[7+8]: 8a861521 CRC32: 32c550f Proof fuer data [5] in Runde 3 Runde 3: CRC32 proof[1-4]: d89aba0d CRC32 proof[2]: 32c550f CRC32: 686159e3 Merkle Tree Root Wert: 686159e3 |
Den Quellcode zum Programm findet Ihr auch zum Download in meinem Github-Repository Timestamping, welches Ihr über diesen Link erreicht: https://github.com/java-crypto/Timestamping. Alle Programme sind unter Java 11 lauffähig (vermutlich auch unter Java 8) und wurden mit intelliJ IDEA entwickelt, welches für dieses Programm aber nicht notwendig ist.
Noch ein Wort zum Thema „Lizenz“: Die von mir erstellten Beispiele stehen unter der „Unlicense“-Lizenz.
Letzte Bearbeitung: 06.05.2020